| c o g n e a t o |
Cogneato Performancetl;drCogneato optimizes a broad set of problems using fewer measurements than other, more specialized tools.
Problems addressed by CogneatoIt is helpful to keep in mind three canonical problems:
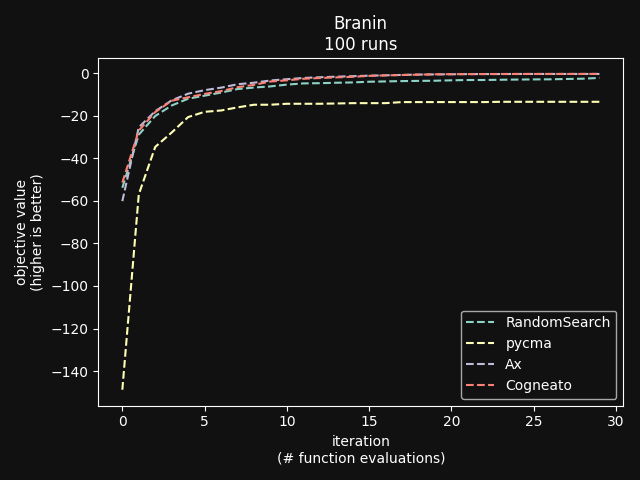
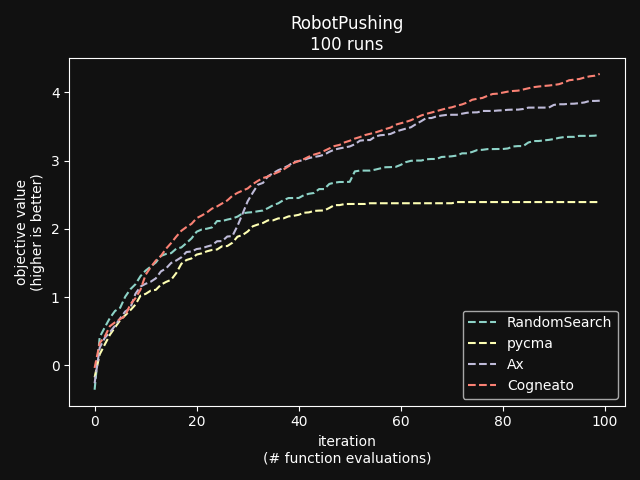
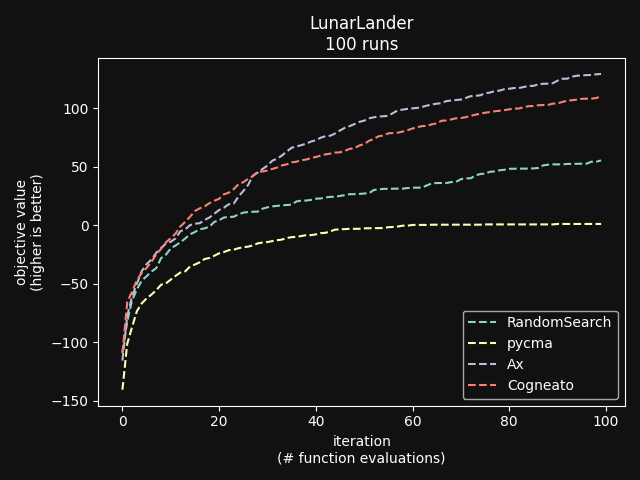
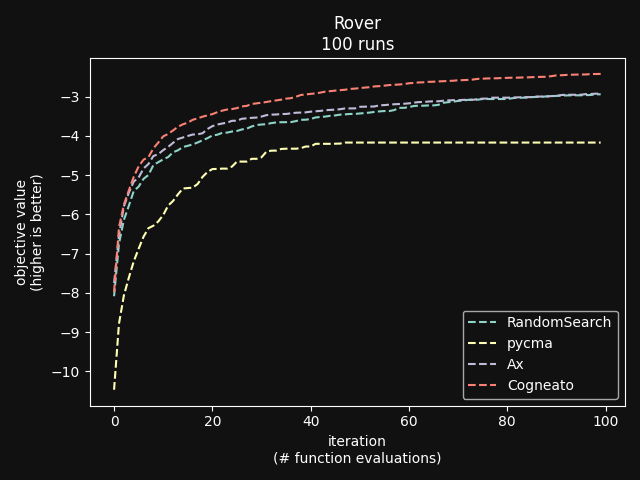
Cogneato is an agglomeration of Bayesian optimization algorithms and techniques engineered to solve problems with a broad range of dimensionality and noise. Cogneato achieves high performance across all three problem types listed above. Performance comparisonsOn tasks where measurements are expensive -- in time, risk, dollars, etc. -- Bayesian optimization outperforms other optimization methods, including grid search, random search, and state-of-the-art evolutionary algorithms [1]. In addition, Bayesian optimization outperforms domain expertise [2]. Below we'll discuss Cogneato's approach to domain expertise and compare its performance to other optimization methods Domain expertiseWhile Bayesian optimization outperforms domain expertise, this doesn't mean that domain expertise has no value. For example, you may have prior experience or fundamental knowledge that can help you identify parameter settings that tend to perform well in your system, or settings that may be dangerous and should be avoided. To incorporate this information, simply include your own measurements in the measurements table along with measurements of parameters suggested by Cogneato. If you are wary of a parameter setting suggested by Cogneato, just exclude it. Cogneato is flexible and will provide the best experiment design based on the measurements you submit. Random searchRandom search, here, refers to choosing parameter settings at random. The choice of parameters does not depend, for example, on previous choices in any way. Varying dimensionalityTo compare Cogneato to random search, we run optimizations on the sphere test function: We execute this entire process once using random search and once using Cogneato. The results are plotted below. 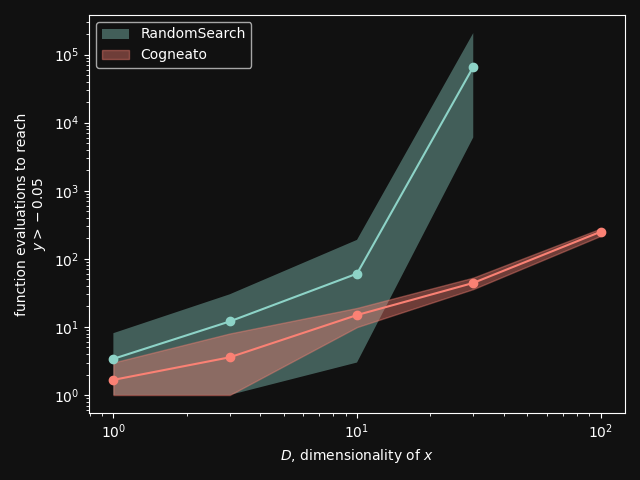 Cogneato reaches the sphere function threshold ( Cogneato reaches the sphere function threshold (y > -0.05) more quickly than random search across a wide range of dimensions.Note that the scales for both axes are logarithmic. No value is plotted for random search at Cogneato outperforms random search for all dimension values -- and by several orders of magnitude when More realistic test functionsThe sphere function is simple to optimize in that it is smooth, noise-free, has one global maximum, and has no local maxima. Below we compare Cogneato to random search using more realistic test functions. Below we plot traces of optimizations, averaged over multiple runs, for both random search and Cogneato 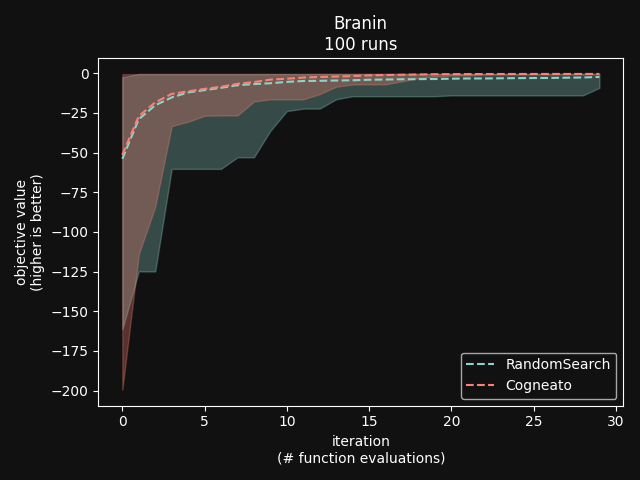 Cogneato reaches a slightly higher objective value than random search when optimizing the 2D Branin test function. Cogneato reaches a slightly higher objective value than random search when optimizing the 2D Branin test function.The Branin function is a 2D test function possessing local minima different from the global minimum. It is commonly used as a test case for Bayesian optimization methods  Cogneato reaches a higher objective value than random search when optimizing the 12D lunar lander controller. Cogneato reaches a higher objective value than random search when optimizing the 12D lunar lander controller.LunarLander[4] is a 12-dimensional task. The objective is to safely land a small spacecraft. It is an RL task, part of OpenAI Gym. In the figure above we are optimizing the parameters of the policy. 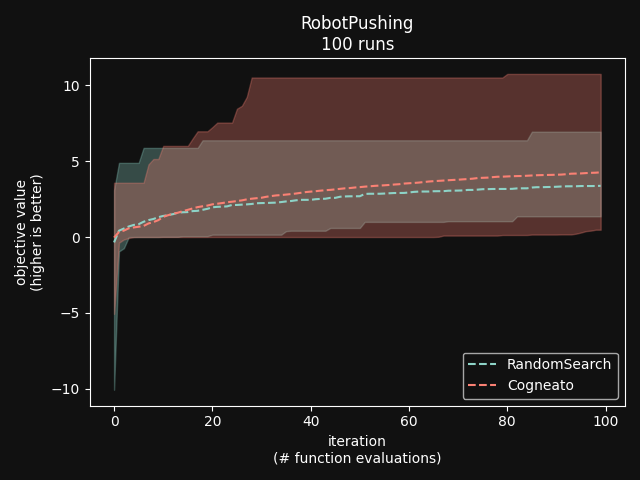 Cogneato reaches a higher objective value than random search when optimizing the 14D robot pushing controller. Cogneato reaches a higher objective value than random search when optimizing the 14D robot pushing controller.Robot pushing[3] is a 14-dimensional task. The objective is to use two robot hands to push two objects toward a goal. Getting closer to the goal yields a higher objective value. This task is implemented in a simulator. 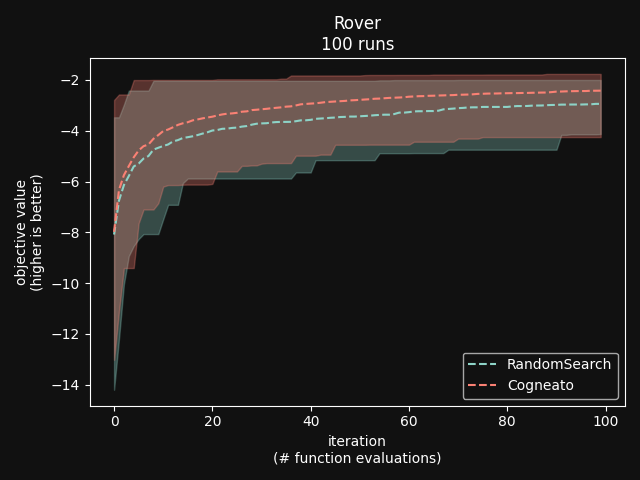 Cogneato reaches a higher objective value than random search when optimizing the 60D Rover navigation problem. Cogneato reaches a higher objective value than random search when optimizing the 60D Rover navigation problem.Rover[3] is a 60-dimensional task. The objective is to plot a course for a rover through a field of obstacles that is as short as possible. It is implemented in a simulator. Cogneato generally outperforms random search. This is consistent with a large-scale study[1] comparing Bayesian optimization to random search more generally. Evolutionary searchThe evolutionary search algorithm CMA-ES[5] is a SOTA block-box optimization algorithm. Its advantages over Bayesian optimization, historically, have been that it (i) calculates the parameter suggestions very quickly, and (ii) scales well to high-dimensional problems. On the other hand, Bayesian optimization has generally performed better when (i) measurements take a long time (> 1 minute, say) or are otherwise costly or risky and thus need to be minimized severely and, thus, the added computation time is warranted, (ii) dimensionality is low (roughly, Recent advances in Bayesian optimization[6] have made higher-dimensional optimizations feasible and have reduced calculation times. Below we compare Cogneato to the open source package pycma. The code works well and reliably over a broad range of optimization problems, and your author has, over the years, made effective use of it for a variety of tasks.  Cogneato reaches the sphere function threshold ( Cogneato reaches the sphere function threshold (y > -0.05) more quickly than pycma across a wide range of dimensions.Note that pycma does not run for 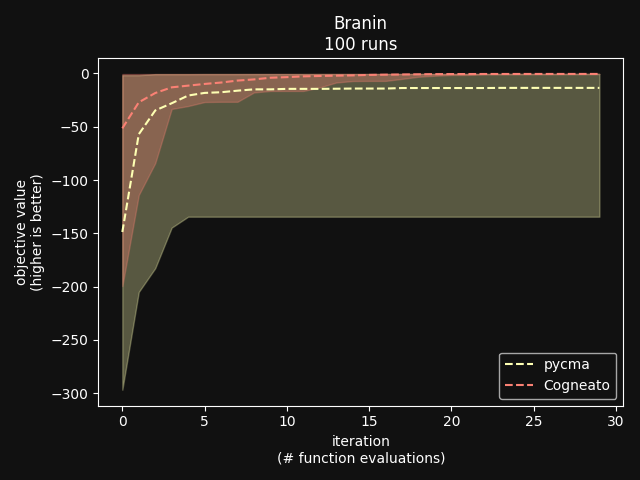 Cogneato performs slightly better than pycma when optimizing the 2D Branin test function. Cogneato performs slightly better than pycma when optimizing the 2D Branin test function.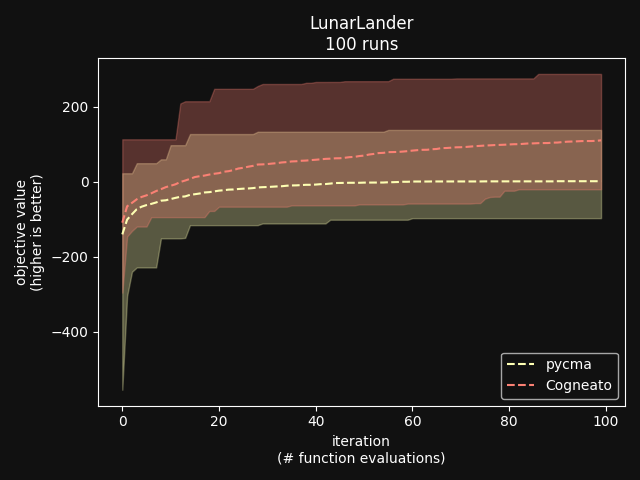 Cogneato outperforms pycma when optimizing the 12D lunar lander controller. Cogneato outperforms pycma when optimizing the 12D lunar lander controller.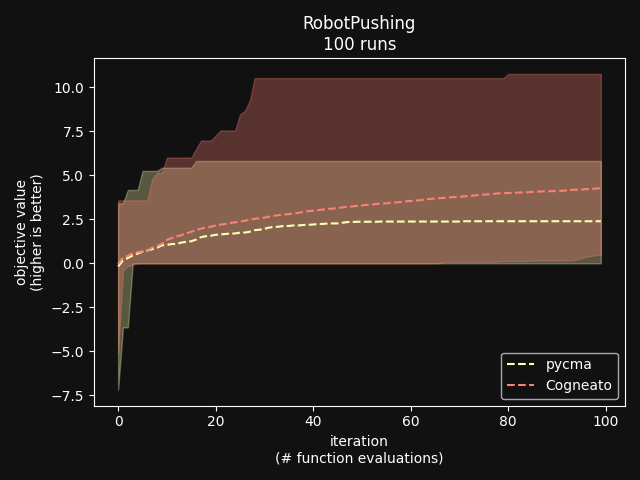 Cogneato outperforms pycma when optimizing the 14D robot pushing controller. Cogneato outperforms pycma when optimizing the 14D robot pushing controller.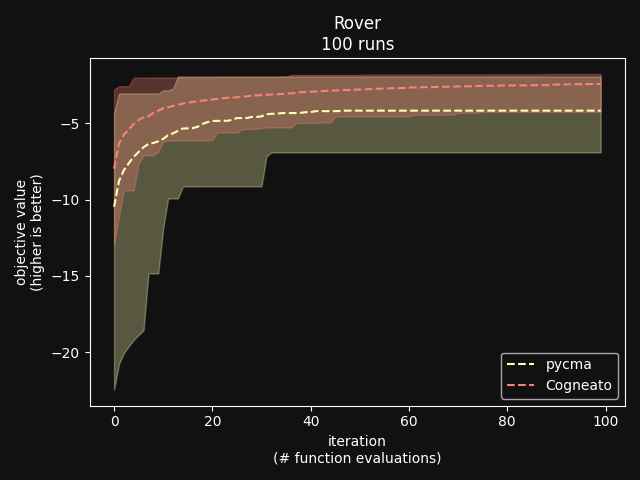 Cogneato outperforms pycma when optimizing the 60D Rover navigation problem. Cogneato outperforms pycma when optimizing the 60D Rover navigation problem.Vanilla Bayesian optimizationCogneato combines multiple SOTA algorithms and techniques from the field of Bayesian optimization into a single optimizer, so we should expect Cogneato to outperform a "vanilla" Bayesian optimizer. We'll compare Cogneato to a default configuration of Ax/BoTorch, an open-source Bayesian optimization package. Ax/BoTorch implements SOTA algorithms, experiment-tracking tooling, and a computation engine built on PyTorch. If you plan to roll your own optimizer, we recommend Ax/BoTorch. In the figures below, we use Ax's
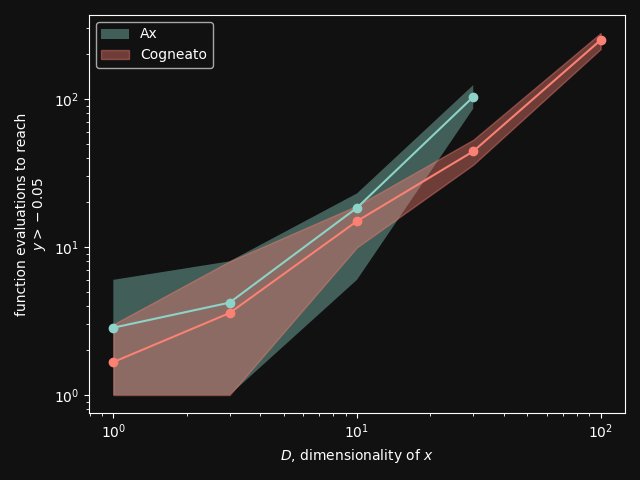 Cogneato reaches the sphere function threshold ( Cogneato reaches the sphere function threshold (y > -0.05) slightly more quickly than Ax's GPEI across a wide range of dimensions.Note that Ax's GPEI does not scale well to higher-dimensional problems. At 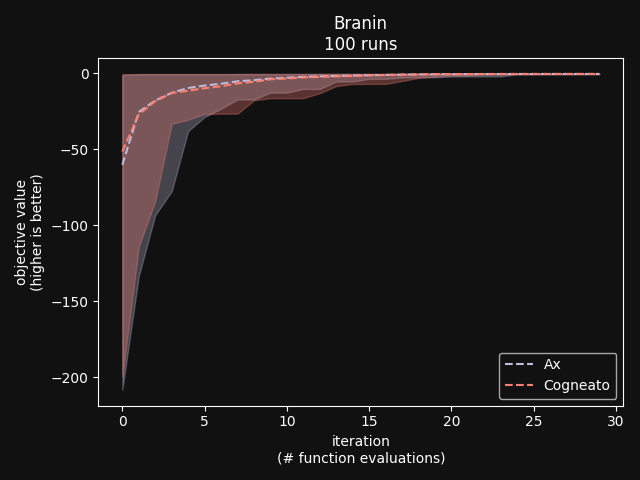 Cogneato performs similarly to Ax when optimizing the 2D Branin test function. Cogneato performs similarly to Ax when optimizing the 2D Branin test function.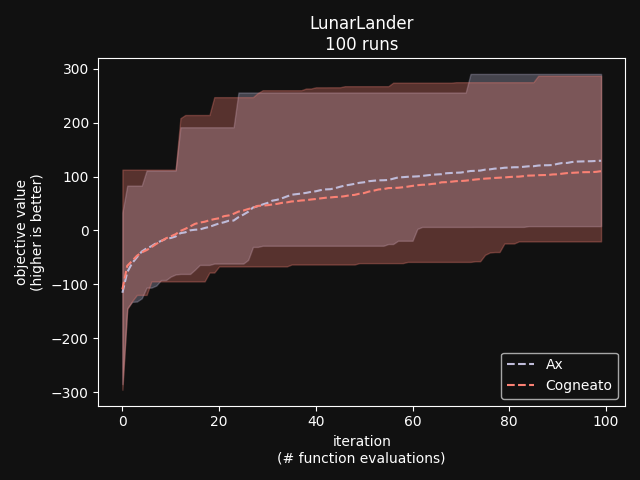 Cogneato performs similarly to Ax when optimizing the 12D lunar lander controller. Cogneato performs similarly to Ax when optimizing the 12D lunar lander controller.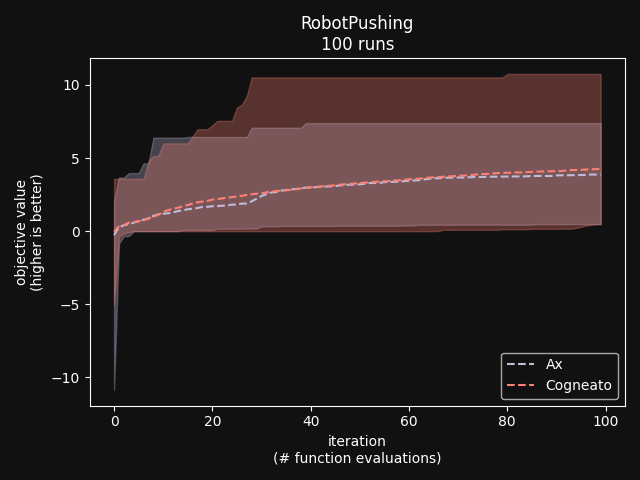 Cogneato performs similarly to Ax when optimizing the 14D robot pushing controller. Cogneato performs similarly to Ax when optimizing the 14D robot pushing controller.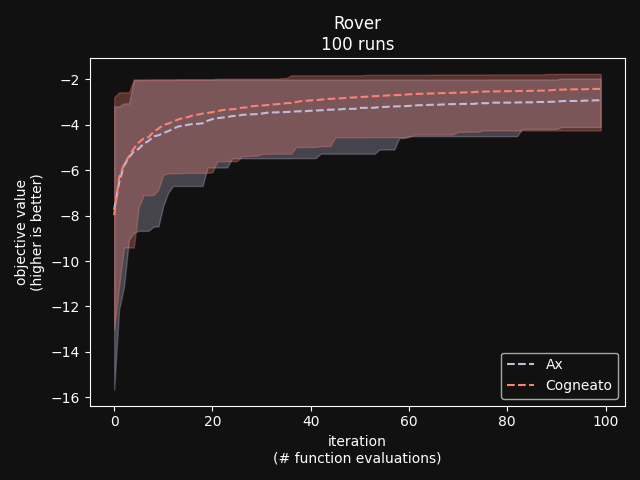 Cogneato outperforms Ax when optimizing the 60D Rover navigation problem. Cogneato outperforms Ax when optimizing the 60D Rover navigation problem.Overall, Cogneato performs similarly to Ax on low-dimensional problems and outperforms it on higher-dimensional problems. References
|
| Copyright © 2024 Vanderdonk, LLC |
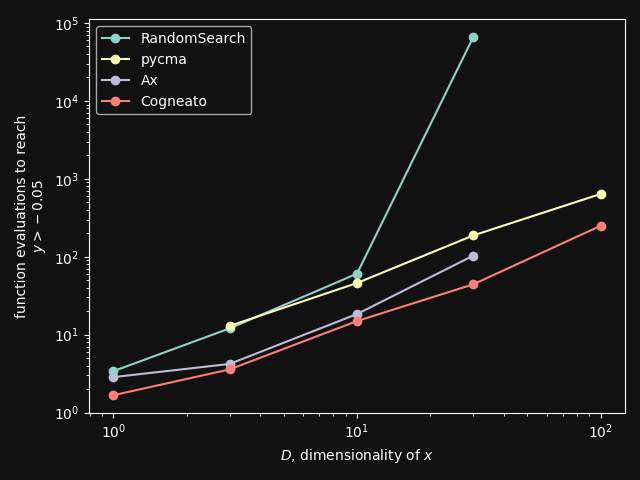 Number of function evaluations require to optimize the sphere function to a threshold value.
Number of function evaluations require to optimize the sphere function to a threshold value.